Albert Einstein once said that Compounding is the Eighth wonder of the world and he who understands it does not pay it. Let us understand why did he tell this and what is the logic behind it, but before that let’s understand what is Compounding. Interest is the additional amount that one pays or gets paid for borrowing or lending money. The basic notion of interest comes from the fact that if one lends money to someone for any economic activity, then the borrower of the money who will earn profits by using someone else’s money should pay him a part of those profits. This is how simple interest work, where the interest is calculated on the principal amount which is the amount borrowed. Compounding Interest is basically interest on interest. So the calculation of interest is not only on the principal amount that is borrowed but also on the interest that keeps on getting accumulated. That major focus over here is on the calculation of interest. Most of the people focus only on the interest rates but rather than focusing on the interest rate one should focus on the number of times the interest is getting compounded. This could work both the ways. Many times financial institution trap their customers by keeping a lower interest rates but compounding them at a higher frequency like compounding every quarter. Similarly the same could work wonders if you are the lender. So rightly said by Albert Einstein, that if you know compounding interest you will never end up paying it more that you earn. Today most the of transaction of lending and borrowing happen at a compounding interest. In the upcoming posts, on our social media we will post some different case studies on how different scenarios work in compounding and each one of us can check on how much they pay more and how much they’ll end up saving if one understands this concept clearly.
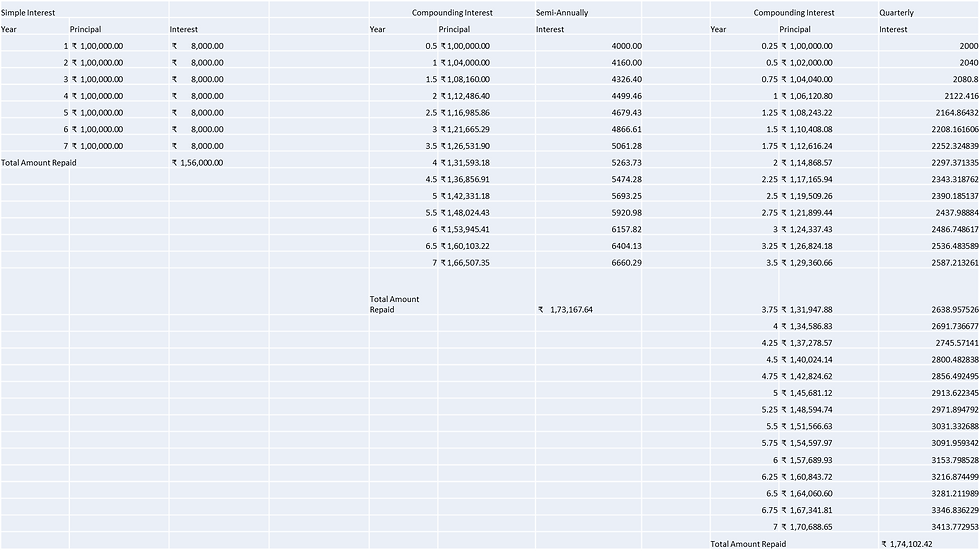
The table below shows the different cases of interest calculation when Principal is Rs. 1,00,000 is borrowed with an interest rate of 8% for 7 years. We see that Simple Interest has the lowest sum accumulated after 7 years compared to compounding interest semi-annually and quarterly. In case of semi-annually we see that the sum comes to 1,73,167.64 and the same when compounded quarterly comes to 1,74,102.42, thus validating our point from the previous page and hence we can conclude that why focusing on the number of time the rate is compounded is more important.

Comments